Loading advertisement...
07-03-2025

As the CBSE Class 12 board exams approach, students often seek effective last-minute revision strategies to maximize their scores. Mathematics, being a subject that demands precision and problem-solving skills, requires rigorous practice. One of the best ways to enhance your preparation is by solving CBSE Class 12 Maths Sample Papers 2025.
Practicing with sample papers is an essential part of exam preparation, offering multiple benefits:
✅ Exam Pattern Familiarity – Sample papers align with the CBSE marking scheme and give you a clear idea of the question types.
✅ Time Management – Solving papers under timed conditions improves speed and accuracy, helping you complete the exam on time.
✅ Identifying Weak Areas – Reviewing mistakes in practice papers helps you focus on topics that need improvement.
✅ Boosts Confidence – Regular practice reduces exam anxiety and enhances problem-solving efficiency.
1. If A =

(a) 5A
(b) 10A
(c) 16A
(d) 32A
2. If A is a square matrix of order 3 such that |A| = 3 then the value of |adj(adjA)|
(a)9
(b) 81
(c) 6
(d) 27
3.

(a)0
(b) 50
(c) 59
(d) 512
4. Find the value of a d/dx (cos2x- sin2x/ cos x + sin x)
(a) Sinx +cosx
(b) - cosx – sinx
(c) −sinx −cosx
(d) sinx -cosx
5. If A2 -A+I =0, then the inverse of A is
(a)A+I
(b)I-A
(c) A-I
(d)I+A
6. If f(x) =
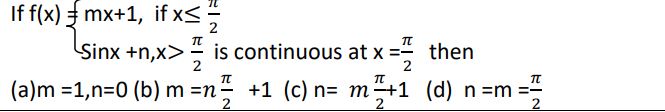
(a)m =1,n=0
(b) m =𝑛 𝜋/2 +1
(c) n= 𝑚 𝜋/2
(d) n =m =𝜋/2
7. If the area of a triangle is 35 sq. units with vertices (2,-6), (5,4) and (k,4) then k is
(a) 12
(b) -2
(c) -12,-2
(d) 12,-2
8. The value of
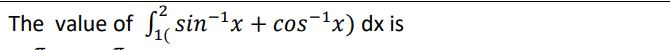
(a) 𝜋/2
(b) - 𝜋/2
(c) 0
(d) 2𝜋
9. Determine the sum of order and degree of the differential equation:

(a) 2
(b) 1
(c) 3
(d) 4
10. Evaluate

(a) tanx + cotx
(b) tanx- cotx +c
(c) 1
(d) -1
11. Solve the differential equation cos(𝑑𝑦/𝑑𝑥) = a, a∈ 𝑅.

Answer: b
12. 𝑎⃗ and 𝑏⃗unit vectors and 𝜃 is the angle between them then 𝑎⃗ + 𝑏⃗ is a unit vector if 𝜃 is equal to
(a) −2𝜋/3
(b) −𝜋/3
(c) 2𝜋/3
(d) 𝜋/3
13. Find the area of a parallelogram whose one diagonal is 2i+j-2k and one side is 3i +j –k
(a) √21
(b) √6
(c) √21/2
(d) 3√2
14. |𝑎⃗ x 𝑏⃗ | 2 + |𝑎⃗. 𝑏⃗ | 2 =400 , |𝑎⃗| = 5 then find the value of |𝑏⃗|
(a) 5
(b) 4
(c) 5√2
(d) √2
15. If objective function Z =px +qy is maximum at (4,-2) and maximum value is 10 such that p = 3q then find p &q
(a) P = 3, q=1
(b) p = -3 q = -1
(c) p=3 , q= -1
(d) p =-3 , q= 1
16. The point which does not lie in the half-plane 2x + 3y -12 < 0 is: (a)(2,1)
(b)(1,2)
(c)(-2,3)
(d)(2,3)
17. A line makes angle α, β, γ with x-axis, y-axis and z-axis respectively, then cos 2α + cos 2β + cos 2γ is equal to
(a) -1
(b) 1
(c) 3
(d) 2
18. An urn contains 10 black and 5 white balls. Two balls are drawn from the urn one after the other without replacement. What is the probability that both drawn balls are black?
(a) 3/7
(b) 7/3
(c) 1/7
(d) ⅓
ASSERTION-REASON BASED QUESTIONS In the following questions, a statement of assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A.
(b) Both A and R are true but R is not the correct explanation of A.
(c) A is true but R is false.
(d) A is false but R is true.
19. Assertion (A) Range of 𝑡𝑎𝑛−1 x is (− 𝜋/2 , 𝜋/2 )
Reason (R) Domain of 𝑡𝑎𝑛−1 x is R
(b) Both A and R are true but R is not the correct explanation of A.
20. Assertion (A) The position vector of a particle in a rectangular coordinate system is (3,2,5) then its position vector is 3𝑖̂+5𝑗̂+ 3 𝑘̂
Reason (R) the displacement vector of the particle that moves from (2,3,5) to the point (3,4,5) is 𝑖̂+𝑗̂
(d) A is false but R is true.
This section comprises of very short answer type-questions (VSA) of 2 marks each.
21. Find the value of 𝑠𝑖𝑛−1 (cos 3𝜋 /5 )
OR
Prove that the f 𝑅 → 𝑅 𝑑𝑒𝑓𝑖𝑛𝑒𝑑 𝑏𝑦 f ( x) = 𝑥3 + 4 is one one and onto
Answer: −𝜋/10 OR Proof
22. If 𝑎⃗ = 𝑖̂+ 𝑗̂− 5𝑘̂ and𝑏⃗=𝑖̂-4 𝑗̂+3 𝑘̂ find a unit vector parallel to 𝑎⃗+𝑏⃗
OR
Find the direction cosines of a line passing through the origin and lying in the first quadrant, making equal angles with the three coordinate axis
Answer:

23. Solve x log x 𝑑𝑦/𝑑𝑥 + y = 2/𝑥 log x
Answer: Y log x = −2/𝑥 (1+logx) +c
24. If |𝑎⃗| = 4 ,|𝑏⃗| = 3 and 𝑎⃗. 𝑏⃗ =6√3 find |𝑎⃗ x 𝑏⃗ |
Answer: 6
25. Water is leaking from a conical funnel at the rate of 5 cubic centimeters per second. if the radius of the base of the funnel is 10 cm and the altitude is 20 cm , find the rate at which the water level is dropping when it is 5cm from the top
Answer: 4/45𝜋
(This section comprises of short answer type questions (SA) of 3 marks each)
26. Evaluate

Answer:
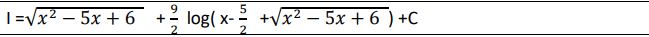
27. Bag A contains 4 black and 6 red balls and Bag B contains 7 black and 3 red balls. A die is thrown if 1 or 2 appears, bag A is chosen, otherwise bag B. If two balls are drawn at random without replacement from the selected bag, find the probability of getting one red and one black.
OR
In a game, a man wins Rs 5 for 6 and loses rupees one for any other number, when a fair die is thrown. The man decided to throw a die thrice but quits as and when he gets a six. Find the expected value of the amount he wins/loses.
Answer: P(E1) = 2/6 , P(E2) = 4/6 , P(A/E1) = 24/45 P(A/E2) = 21/45 ,P(A) = 22/45
OR
X = 4,3,-3 P(x=5) =1/6 , P(x=4) = 5/36 , P(x=3) = 25/216 , P(x=-3) =125/216 ,E(x)=0
28. 𝐸𝑣𝑎𝑙𝑢𝑎𝑡𝑒 ∫ 𝑡𝑎𝑛−1 x dx
Answer:

29. Evaluate
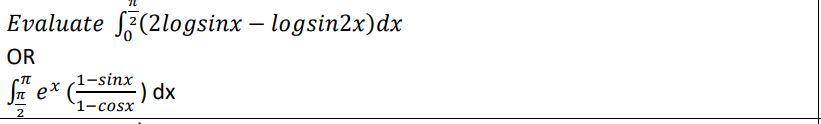
Answer:

30. Maximise Z = 80x +120y subject to constraints 9x +12y ≤ 180 , 3𝑥 + 4𝑦 ≤ 60, 𝑥 + 3𝑦 ≤ 30, 𝑥 ≥ 0 𝑦 ≥ 0.
Answer: Max Z= 1680 and max point is (12,6)
31. Solve
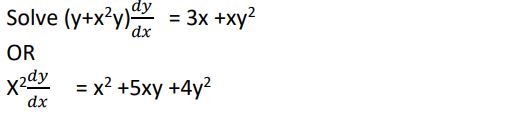
Answer:

(This section comprises of long answer-type questions (LA) of 5 marks each)
32. If A=

Answer: X= 2, y= -1, z= 4
33. Find the area of the region { (x,y) : 𝑥2 + 𝑦 2 ≤ 4 , x + y ≥ 2 } using integration.
Answer:
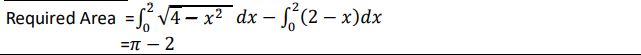
34. Let N be the set of all natural numbers and R be a relation defined by (𝑎, 𝑏) 𝑅 (𝑐, 𝑑)) If bc(a+d) = ad(b+c). show that R is an equivalence relation.
Answer: Proof
35. Find the points on the line 𝑥+2 3 = 𝑦+1 2 = 𝑧−3 2 at a distance of 5 units from the point ( 1,3,3 )
OR
Find the foot of the perpendicular from ( 0,2,3 ) on the line 𝑟⃗ = -3𝑖̂ + 𝑗̂-4𝑘̂ +k(5𝑖̂ + 2 𝑗̂+3𝑘̂ )
Answer: Points are (-2,-1,3) and (4,3,7)
OR
K =1, Point is (2,3,-1)
36. A telephone company in a town has 500 subscribers on its list and collects fixed charges of 300 per subscriber per year. The company proposes to increase the annual subscription and it is believed that for every increase of 1 one subscriber, one will discontinue the service.
(i) If x be the annual subscription, then the total revenue of the company after increment will be
(ii) How much fee the company should increase to have maximum profit.
Correct Answer:
(i) R(x)= (500-x)(300+x) = –x 2+200x+150000
(ii) 100
37. One day, a sangeet mahotsav is to be organised in an open area of Rajasthan. In recent years, it has rained only 6 days each year. Also, it is given that when it actually rains, the weatherman correctly forecasts rain 80% of the time. When it doesn’t rain, he incorrectly forecasts rain 20% of the time. If leap year is considered, then answer the following questions.
(i) The probability that it rains on a chosen day is
(ii) The probability that it does not rain on the chosen day is
(iii) The probability that the weatherman predicts correctly is
(iv) The probability that it will rain on the chosen day, if the weatherman predicts rain for that day, is
Correct Answer:
(i) 1/61
(ii) 60/61
(iii) 4/5
(iv) 0.94
38. The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x-1/2 x2 where x is the number of days exposed to sunlight.
(i) The rate of growth of the plant with respect to sunlight is
(ii) What is the number of days it will take for the plant to grow to the maximum height?
(iii) What is the maximum height of the plant?
(iv) If the height of the plant is 7/2 cm, the number of days it has been exposed to the sunlight is
Correct Answer:
(i) 4 – x
(ii) 4
(iii) 8cm
Follow these steps to make the most of your practice sessions:
📌 Solve at Least One Sample Paper Daily – This builds consistency and strengthens conceptual clarity.
📌 Stick to the Exam Time Limit – Practice in a real exam-like environment to enhance speed and accuracy.
📌 Analyze Your Mistakes – Identify errors, revise weak areas, and work on improving them.
📌 Revise NCERT Problems – Since CBSE largely follows NCERT, ensure you have mastered all NCERT exercises and examples.
📌 Focus on High-Weightage Topics – Prioritize important chapters like Calculus, Algebra, and Probability to maximize your score.
With strategic last-minute revision and consistent practice using CBSE Class 12 Maths 2025 Sample Papers, you can boost your confidence and improve your chances of scoring high in the exam. Stay focused, practice smartly, and give your best on the exam day!
Also Check:
| Year | Link |
|---|---|
| 2022 | Click Here |
| 2023 | Click Here |
| 2024 | Click Here |
All the best for your CBSE Class 12 Maths exam! 🎯📖✏️