1. In the figure, O is the center of the circle. If ∠ACB = 70°,

(a) Find ∠AOB
(b) Find ∠ADB

Given ∠ACB = 70°

(a) Finding ∠AOB:

The angle subtended by an arc

at the center is twice the angle 

subtended at any point on the 

circumference.

Hence, ∠AOB = 2 × ∠ACB
= 2 × 70°
= 140°

Answer: ∠AOB = 140°

(b) Finding ∠ADB:

The angles subtended by the same

chord on the same side of the

circle are equal.

Therefore, ∠ADB = ∠ACB
= 70°

∠ADB = 70°

2. Given the arithmetic sequence: 3, 8, 13, ...

(a) Find the common difference (d)
(b) Find the 11th term of the sequence

(a) Finding the Common Difference (d):

The common difference 

d is given by:
d = second term - first term
    = 8 - 3 = 5

Answer: Common difference (d) = 5

(b) Finding the 11th Term:

The formula for the nth term of 

an arithmetic sequence is:

an=a+(n−1)d

where:

• a = 3 (first term)
• d = 5 (common difference)
• n = 11

a11=3+(11−1)×5 =3+10×5= 3+50= 53

 11th term = 53

3. Numbers from 1 to 20 are written on paper slips and put in a box. A slip is drawn at random.

(a) What is the probability that it is a prime number?
(b) What is the probability that it is a perfect square?

(a) Probability of Prime Number:

Prime numbers between 1 and 20:

 2, 3, 5, 7, 11, 13, 17, 19

Total prime numbers = 8

Total numbers = 20

P(prime number) = number of 

favourable outcomes/total outcomes

= 8/20 = 2/5

Answer: 2/5

(b) Probability of a Perfect Square:

• Perfect squares between 1 and 20: 1, 4, 9, 16
• Total perfect squares = 4
• Total numbers = 20

P(perfect square)=number of 

favorable outcomes/total outcomes

=4/20=1/5

Answer: 1/5

4.

In the figure, O is the center of the circle. Given BC = 4 cm and ∠A = 50°, find the diameter of the circle.
(Trigonometric values given: sin 50° = 0.77, cos 50° = 0.64)

In the given figure, BC is the chord of the circle.

Since O is the center, OB = OC (radii of the circle), 

and ∠A = 50°  (given)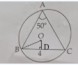

The perpendicular from O to BC bisects BC, 

so the half-length of BC is 2 cm.

Or BD = 2 cm

We use the formula: 

• OB=BD/cos50∘ = 2/0.64 = 3.125 cm
• The diameter is 2 × OB
• Diameter= 2×3.125=6.25 cm

Answer: Diameter = 6.25 cm

5. 6 times of a natural number subtracted from the square of that number gives 187.

(a) Form a quadratic equation.
(b) Find the number.

Let the natural number be x.

(a) Given:

x2−6x=187

Rearranging:

x2−6x−187=0

Answer: Quadratic equation: x2−6x−187=0

(b) Solving for x using the quadratic formula:

So, the valid answer is x = 17.

Answer: Natural number = 17

6. Given two points (2,5) and (3,7)

(a) Find the slope of the line.
(b) Write the equation of the line.

(a) Slopeof the line is given as:

m=(y2−y1)/(x2−x1)

=(7−5)/(3−2)=2/1=2

Answer: Slope = 2

(b) Equation of the line using

y−y1=m(x−x1)

y−5=2(x−2)= 

y−5=2x−4

y=2x+1

Answer: Equation: y=2x+1

7. Consider the arithmetic sequence 2, 8, 14, ...

(a) What is the remainder when terms of this sequence are divided by 6?
(b) Is 176 a term of this sequence? Why?

(a) Finding Remainders:

• First term 2 mod 6 = 2
• Second term 8 mod 6 = 2
• Third term 14 mod 6 = 2

Since all terms leave a remainder 2,

the remainder is always 2.

Answer: Remainder = 2

(b) Checking if 176 is a term:

Formula for nth term:

an=a+(n−1)d

a = 2, d = 6, a_n = 176

176=2+(n−1)×6

176−2=(n−1)×6

174=(n−1)×6

(n-1)= 174/6=29

n=30

Since n = 30 is a whole number, 

176 is a term of the sequence.

Answer: Yes, 176 is a term

8. In the figure, PA = 8 cm, AB = 3 cm, PC = 10 cm.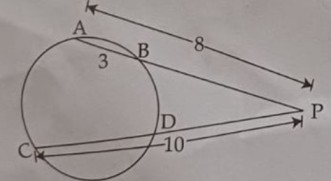

(a) Find the length of PB.
(b) Find the length of PD.

(a) Using the intercept theorem:

PB=PA−AB

PB=8−3=5

Answer: PB = 5 cm

For PD, using the property 

of intersecting secants:

PA×PB=PC×PD

8×5=10×PD

40 =10×PD

PD=4

Answer: PD = 4 cms

     Kerala Board SSLC Class 10th Maths  Answer Key 2025